Chaos Theory
A BRIEF INTRODUCTION TO
CHAOS THEORY
BY GREGORY RAE
WHAT EXACTLY IS CHAOS?
The name “chaos theory” comes from the fact that the systems that the theory describes are apparently disordered, but chaos theory is really about finding the underlying order in apparently random data.
WHEN WAS CHAOS FIRST DISCOVERED?
The first true experimenter in chaos was a meteorologist named Edward Lorenz. In 1960, he was working on the problem of weather prediction. He had a computer set up with a set of twelve equations to model the weather. It didn’t predict the weather itself. However this computer program did theoretically predict what the weather might be.
One day in 1961, he wanted to see a particular sequence again. To save time, he started in the middle of the sequence, instead of the beginning. He entered the number off his printout and left to let it run.
When he came back an hour later, the sequence had evolved differently. Instead of the same pattern as before, it diverged from the pattern, ending up wildly different from the original. (See Figure 1.)
Eventually he figured out what happened.
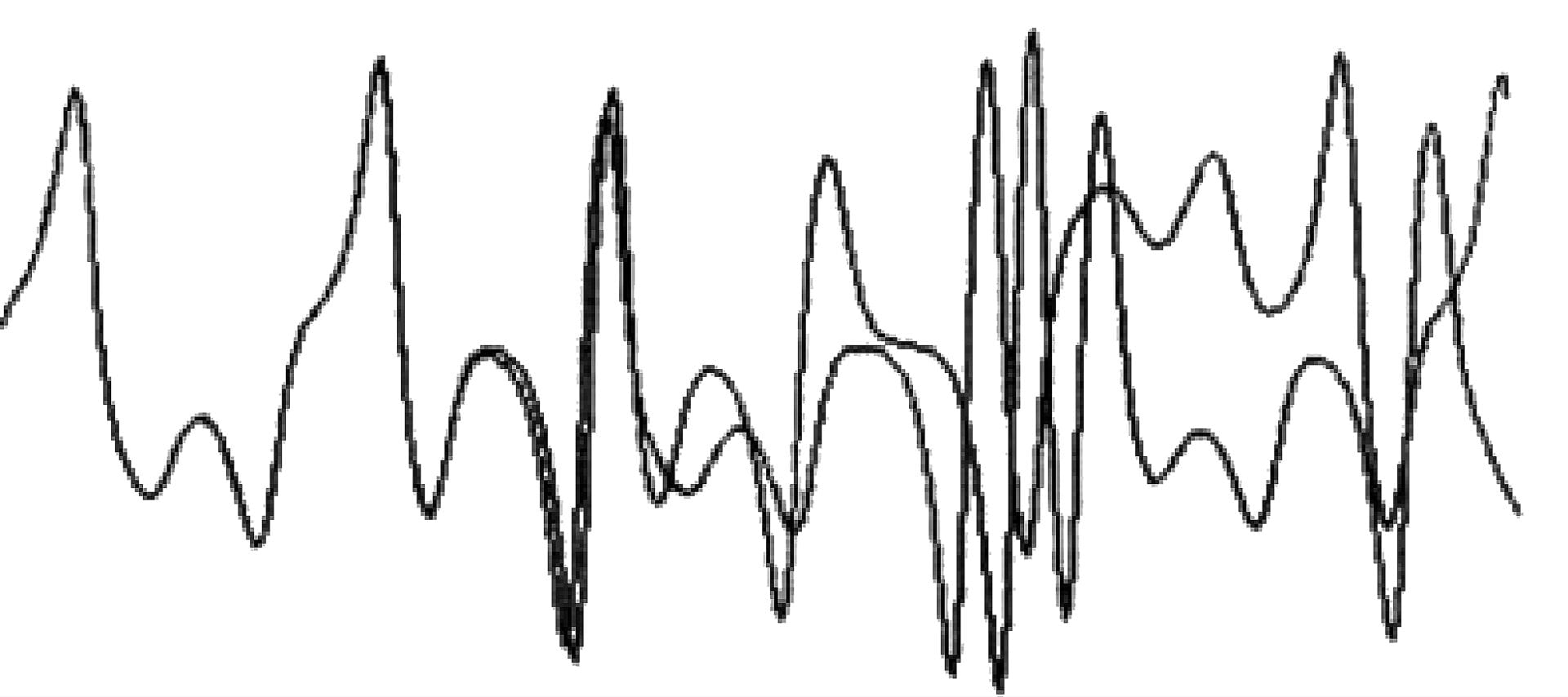
the starting values of these curves is only .000127
(Ian Stewart, “Does God Play Dice?” The Mathematics of Chaos, pg. 141)
The computer stored the numbers to six decimal places in its memory. To save paper, Lorenz only had it print out three decimal places. In the original sequence, the number was .506127, and he had only typed the first three digits, .506. In Lorenz’s experiment, the difference between the starting values of these curves was only .000127.
By all conventional ideas of the time, it should have worked. He should have gotten a sequence very close to the original sequence.
A scientist considers himself lucky if he can get measurements with accuracy to three decimal places. Surely the fourth and fifth, impossible to measure using reasonable methods, can’t have a huge effect on the outcome of the experiment. Lorenz proved this idea wrong.
THIS EFFECT CAME TO BE KNOWN AS THE BUTTERFLY EFFECT.
The amount of difference in the starting points of the two curves is so small that it is comparable to a butterfly flapping its wings.
“The flapping of a single butterfly’s wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month’s time, a tornado that would have devastated the Indonesian coast doesn’t happen. Or maybe one that wasn’t going to happen, does.” (Ian Stewart, “Does God Play Dice?” The Mathematics of Chaos, pg. 141)
This phenomenon, common to chaos theory, is also known as sensitive dependence on initial conditions. Just a small change in the initial conditions can drastically change the longterm behavior of a system.
Such a small amount of difference in a measurement might be considered experimental noise, background noise, or an inaccuracy of the equipment.
Such things are impossible to avoid in even the most isolated lab. With a starting number of 2, the final result can be entirely different from the same system with a starting value of 2.000001.
It is simply impossible to achieve this level of accuracy - just try and measure something to the nearest millionth of an inch!
From this idea, Lorenz stated that it is impossible to predict the weather accurately. However, this discovery led Lorenz on to other aspects of what eventually came to be known as chaos theory.
LORENZ STARTED TO LOOK FOR A SIMPLER SYSTEM…
…that had sensitive dependence on initial conditions. His first discovery had twelve equations, and he wanted a much more simple version that still had this attribute. He took the equations for convection, and stripped them down, making them unrealistically simple.
The system no longer had anything to do with convection, but it did have sensitive dependence on its initial conditions, and there were only three equations this time. Later, it was discovered that his equations precisely described a water wheel.
“At the top, water drips steadily into containers hanging on the wheel’s rim. Each container drips steadily from a small hole. If the stream of water is slow, the top containers never fill fast enough to overcome friction, but if the stream is faster, the weight starts to turn the wheel. The rotation might become continuous. Or if the stream is so fast that the heavy containers swing all the way around the bottom and up the other side, the wheel might then slow, stop, and reverse its rotation, turning first one way and then the other.” (James Gleick, Chaos: Making a New Science, pg. 29)
(James Gleick, Chaos: Making a New Science, pg. 29)
The equations for this system also seemed to give rise to entirely random behavior.
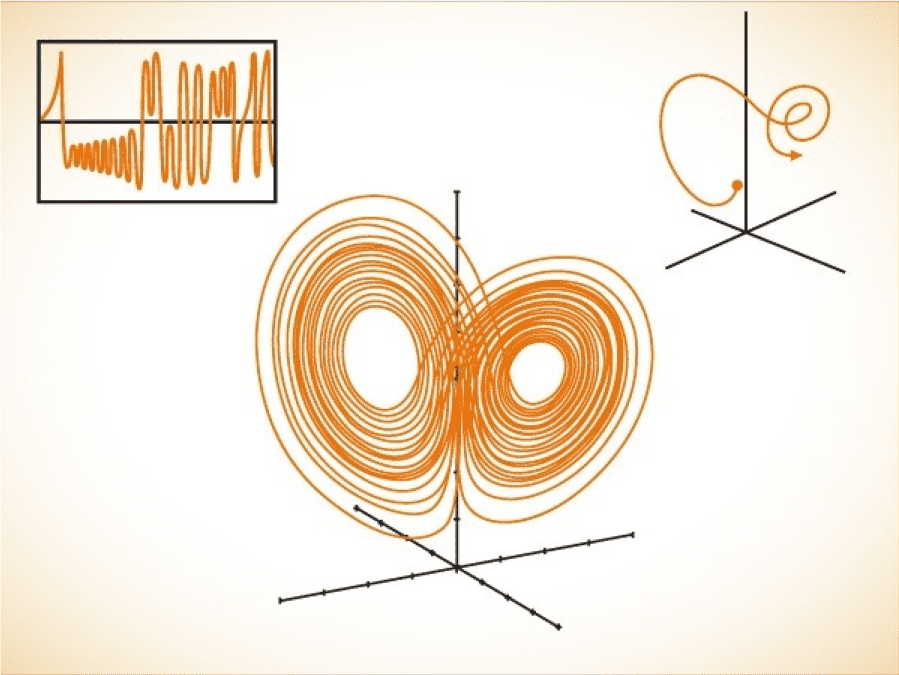
However, when he graphed it, a surprising thing happened. The output always stayed on a curve, a double spiral.
There were only two kinds of order previously known: a steady state, in which the variables never change, and periodic behavior, in which the system goes into a loop, repeating itself indefinitely.
Lorenz’s equations were definitely ordered - they always followed a spiral. They never settled down to a single point, but since they never repeated the same thing, they weren’t periodic either. He called the image he got when he graphed the equations the Lorenz attractor.
In 1963, Lorenz published a paper describing what he had discovered. He included the unpredictability of the weather, and discussed the types of equations that caused this type of behavior.
Unfortunately, the only journal he was able to publish in was a meteorological journal, because he was a meteorologist, not a mathematician or a physicist.
AS A RESULT, LORENZ’S DISCOVERIES WEREN’T ACKNOWLEDGED…
…until years later, when they were rediscovered by others. Lorenz had discovered something revolutionary; now he had to wait for someone to discover him.
Another system in which sensitive dependence on initial conditions is evident is the flip of a coin. There are two variables in a flipping coin: how soon it hits the ground, and how fast it is flipping.
Theoretically, it should be possible to control these variables entirely and control how the coin will end up. In practice, it is impossible to control exactly how fast the coin flips and how high it flips. It is possible to put the variables into a certain range, but it is impossible to control it enough to know the final results of the coin toss.
A similar problem occurs in ecology, and the prediction of biological populations. The equation would be simple if population just rises indefinitely, but the effect of predators and a limited food supply make this equation incorrect. The simplest equation that takes this into account is the following:
next year’s population = r * this year’s population * (1 - this year’s population)
In this equation, the population is a number between 0 and 1, where 1 represents the maximum possible population and 0 represents extinction. R is the growth rate. The question was, how does this parameter affect the equation?
The obvious answer is that a high growth rate means that the population will settle down at a high population, while a low growth rate means that the population will settle down to a low number. This trend is true for some growth rates, but not for every one.
(James Gleick,Chaos: Making a New Science pg. 71)
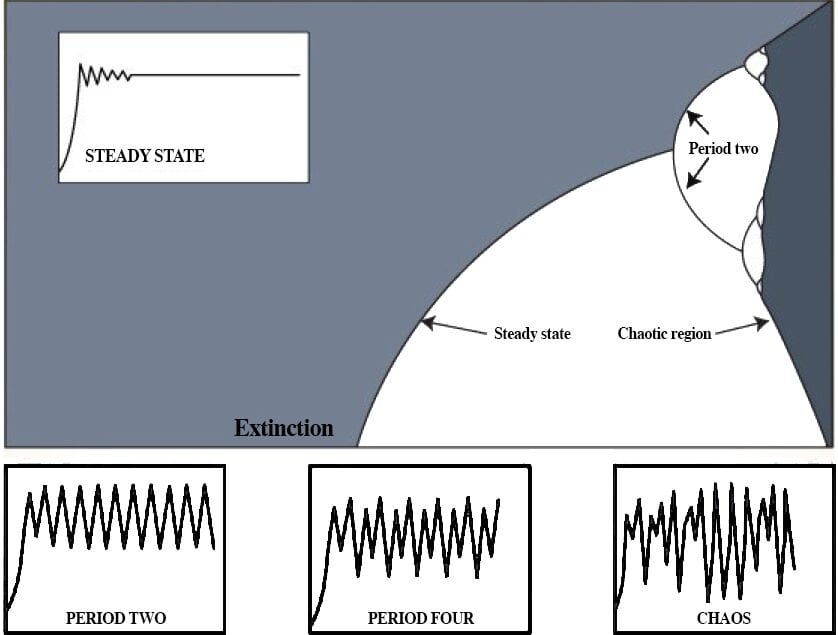
One biologist, Robert May, decided to see what would happen to the equation as the growth rate value changes. At low values of the growth rate, the population would settle down to a single number.
For instance, if the growth rate value is 2.7, the population will settle down to .6292. As the growth rate increased, the final population would increase as well.
Then, something weird happened. As soon as the growth rate passed 3, the line broke in two. Instead of settling down to a single population, it would jump between two different populations. It would be
one value for one year, go to another value the next year, then repeat the cycle forever.
Raising the growth rate a little more caused it to jump between four different values. As the parameter rose further, the line bifurcated (doubled) again. The bifurcations came faster and faster until suddenly, chaos appeared. Past a certain growth rate, it becomes impossible to predict the behavior of the equation.
However, upon closer inspection, it is possible to see white strips. Looking closer at these strips reveals little windows of order, where the equation goes through the bifurcations again before returning to chaos. This self-similarity, the fact that the graph has an exact copy of itself hidden deep inside, came to be an important aspect of chaos.
AN EMPLOYEE OF IBM, BENOIT MANDELBROT…
…was a mathematician studying this self-similarity. One of the areas he was studying was cotton price fluctuations. No matter how the data on cotton prices was analyzed, the results did not fit the normal distribution. Mandelbrot eventually obtained all of the available data on cotton prices, dating back to 1900.
WHEN MANDELBROT ANALYZED THE DATA WITH IBM’S COMPUTERS, HE NOTICED AN ASTONISHING FACT:
“The numbers that produced aberrations from the point of view of normal distribution produced symmetry from the point of view of scaling. Each particular price change was random and unpredictable. But the sequence of changes was independent on scale: curves for daily price changes and monthly price changes matched perfectly. Incredibly, analyzed Mandelbrot’s way, the degree of variation had remained constant over a tumultuous sixty-year period that saw two World Wars and a depression.” (James Gleick, Chaos: Making a New Science, pg. 86)
Mandelbrot analyzed not only cotton prices, but many other phenomena as well. At one point, he was wondering about the length of a coastline. A map of a coastline will show many bays. However, measuring the length of a coastline off a map will miss minor bays that were too small to show on the map.
Likewise, walking along the coastline misses microscopic bays in between grains of sand. No matter how much a coastline is magnified, there will be more bays visible if it is magnified more.
ONE MATHEMATICIAN, HELGE VON KOCH…
…captured this idea in a mathematical construction called the Koch curve. To create a Koch curve, imagine an equilateral triangle. To the middle third of each side, add another equilateral triangle. Keep on adding new triangles to the middle part of each side, and the result is a Koch curve. A magnification of the Koch curve looks exactly the same as the original. It is another self-similar figure.

(James Gleick, Chaos: Making a New Science, pg. 99)
The Koch curve brings up an interesting paradox. Each time new triangles are added to the figure, the length of the line gets longer. However, the inner area of the Koch curve remains less than the area of a circle drawn around the original triangle. Essentially, it is a line of infinite length surrounding a finite area.
To get around this difficulty, mathematicians invented fractal dimensions. Fractal comes from the word fractional. The fractal dimension of the Koch curve is somewhere around 1.26.
A FRACTIONAL DIMENSION IS IMPOSSIBLE TO CONCEIVE, BUT IT DOES MAKE SENSE.
The Koch curve is rougher than a smooth curve or line, which has one dimension. Since it is rougher and more crinkly, it is better at taking up space. However, it’s not as good at filling up space as a square with two dimensions is, since it doesn’t really have any area. So it makes sense that the dimension of the Koch curve is somewhere in between the two.
Fractal has come to mean any image that displays the attribute of self-similarity. The bifurcation diagram of the population equation is fractal. The Lorenz Attractor is fractal. The Koch curve is fractal.
During this time, scientists found it very difficult to get work published about chaos. Since they had not yet shown the relevance to real-world situations, most scientists did not think the results of experiments in chaos were important.
As a result, even though chaos is a mathematical phenomenon, most of the research into chaos was done by people in other areas, such as meteorology and ecology. The field of chaos sprouted up as a hobby for scientists working on problems that maybe had something to do with it.
Later, a scientist by the name of Feigenbaum was looking at the bifurcation diagram again. He was looking at how fast the bifurcations come. He discovered that they come at a constant rate. He calculated it as 4.669.
In other words, he discovered the exact scale at which it was self-similar. Make the diagram 4.669 times smaller, and it looks like the next region of bifurcations.
He decided to look at other equations to see if it was possible to determine a scaling factor for them as well. Much to his surprise, the scaling factor was exactly the same. Not only was this complicated equation displaying regularity, the regularity was exactly the same as a much simpler equation. He tried many other functions, and they all produced the same
scaling factor, 4.669.
THIS WAS A REVOLUTIONARY DISCOVERY.
Feigenbaum had found that a whole class of mathematical functions behaved in the same, predictable way. This universality would help other scientists easily analyze chaotic equations. Universality gave scientists the first tools to analyze a chaotic system. Now they could use a simple equation to predict the outcome of a more complex equation.
Many scientists were exploring equations that created fractal equations. The most famous fractal image is also one of the most simple. It is known as the Mandelbrot set. The equation is simple: z = z2+c. To see if a point is part of the Mandelbrot set, just take a complex number z. Square it, then add the original number. Square the result, then add the original number.
Repeat that ad infinitum, and if the number keeps on going up to infinity, it is not part of the Mandelbrot set. If it stays down below a certain level, it is part of the Mandelbrot set. The Mandelbrot set is the innermost section of the picture, and each different shade of gray represents how far out that particular point is.
One interesting feature of the Mandelbrot set is that the circular humps match up to the bifurcation graph. The Mandelbrot fractal has the same self-similarity seen in the other equations. In fact, zooming in deep enough on a Mandelbrot fractal will eventually reveal an exact replica of the Mandelbrot set, perfect in every detail.
FRACTAL STRUCTURES HAVE BEEN NOTICED IN MANY REAL-WORLD AREAS…
…as well as in mathematician’s minds. Blood vessels branching out further and further, the branches of a tree, the internal structure of the lungs, graphs of stock market data, and many other real-world systems all have something in common: they are all self-similar.
Scientists at UC Santa Cruz found chaos in a dripping water faucet. By recording a dripping faucet and recording the periods of time, they discovered that at a certain flow velocity, the dripping no longer occurred at even times. When they graphed the data, they found that the dripping did indeed follow a pattern.
THE HUMAN HEART ALSO HAS A CHAOTIC PATTERN.
The time between beats does not remain constant; it depends on how much activity a person is doing, among other things. Under certain conditions, the heartbeat can speed up. Under different conditions, the heart beats erratically. It might even be called a chaotic heartbeat.
The analysis of a heartbeat can help medical researchers find ways to put an abnormal heartbeat back into a steady state, instead of uncontrolled chaos.
Researchers discovered a simple set of three equations that graphed a fern. This started a new idea - perhaps DNA encodes not exactly where the leaves grow, but a formula that controls their distribution. DNA, even though it holds an amazing amount of data, could not hold all of the data necessary to determine where every cell of the human body goes.
However, by using fractal formulas to control how the blood vessels branch out and the nerve fibers get created, DNA has more than enough information. It has even been speculated that the brain itself might be organized somehow according to the laws of chaos.
CHAOS EVEN HAS APPLICATIONS OUTSIDE OF SCIENCE.
Computer art has become more realistic through the use of chaos and fractals. Now, with a simple formula, a computer can create a beautiful, and realistic tree. Instead of following a regular pattern, the bark of a tree can be created according to a formula that almost, but not quite, repeats itself.
MUSIC CAN BE CREATED USING FRACTALS AS WELL.
Using the Lorenz attractor, Diana S. Dabby, a graduate student in electrical engineering at the Massachusetts Institute of Technology, has created variations of musical themes. (“Bach to Chaos: Chaotic Variations on a Classical Theme”, Science News, Dec. 24, 1994)
By associating the musical notes of a piece of music like Bach’s Prelude in C with the x coordinates of the Lorenz attractor, and running a computer program, she has created variations of the theme of the song. Most musicians who hear the new sounds believe that the variations are very musical and creative.
CHAOS HAS ALREADY HAD A LASTING EFFECT ON SCIENCE…
…yet there is much still left to be discovered. Many scientists believe that twentieth century science will be known for only three theories: relativity, quantum mechanics, and chaos.
Aspects of chaos show up everywhere around the world, from the currents of the ocean and the flow of blood through fractal blood vessels to the branches of trees and the effects of turbulence. Chaos has inescapably become part of modern science. As chaos changed from a little-known theory to a full science of its own, it has received widespread publicity.
Chaos theory has changed the direction of science: in the eyes of the general public, physics is no longer simply the study of subatomic particles in a billion-dollar particle accelerator, but the study of chaotic systems and how they work.
BIBLIOGRAPHY
“Bach to Chaos: Chaotic Variations on a Classical Theme”, Science News, Dec. 24, 1994, pg. 428.
Gleick, James, Chaos: Making a New Science, Penguin Books Ltd, Harmondsworth, Middlesex, 1987.
Lowrie, Peter, personal interview over the Internet, May 17, 1995.
Rae, Kevin, “Chaos”, unpublished paper, submitted to Professor Gould, Modern Physics
class, Claremont McKenna College, December 5, 1994.
Stewart, Ian, Does God Play Dice? The Mathematics of Chaos, Penguin Books Ltd,
Harmondsworth, Middlesex, 1989.
I’d also like to thank David Harrison, from the University of Toronto Department of
Physics for some suggestions in rewording my introduction (May 17, 2004).
NOTE BY GREGORY RAE
“Although this paper was written at a time when it would have been possible to do some research online, part of the paper requirements were that no online resources were used. We were required to have at least one personal interview (which I had to conduct over e-mail, given my lack of contact with experts on chaos theory at the time). Also, my brother had written a paper on the subject for one of his college physics classes. The paper quotes from original sources a lot more than I would if writing the same thing today, but part of the assignment was to write a research paper and properly cite all sources.”
(REMARKABLY, GREGORY RAE WROTE THIS SIMPLE, CLEAR, AND ACCURATE INTRODUCTION TO CHAOS THEORY WHEN HE WAS IN HIGH SCHOOL.)
